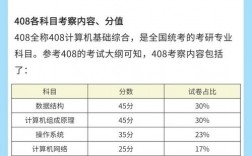
2024年考研数学二的考试内容主要包括以下几个部分:
1. 高等数学(约占试卷的80%)

- 函数、极限、连续性
- 导数与微分
- 不定积分与定积分
- 多元函数微积分
2. 线性代数(约占试卷的20%)
- 行列式的概念和基本性质
- 矩阵的运算及其性质
- 线性方程组的解法
- 特征值及其应用
3. 考试形式
- 试卷满分为150分,考试时间为180分钟。
- 题型结构包括单项选择题、填空题和解答题。
具体的考试要求包括:
- 理解函数的概念及其性质,掌握极限的运算和存在准则。
- 掌握导数的几何意义,能够求解简单的微分和积分问题。
- 了解多元函数的偏导数和全微分的概念。
- 理解线性代数中的矩阵运算和行列式的性质。
建议考生根据这些内容制定复习计划,以便更好地准备考试。
数二考研范围
2024年考研数学二的考试范围主要包括两个部分:高等数学和线性代数。以下是具体的考试内容:
高等数学部分
1. 函数、极限、连续
- 函数的概念及表示法
- 函数的有界性、单调性、周期性和奇偶性
- 复合函数、反函数、分段函数和隐函数
- 基本初等函数的性质及其图形
- 初等函数
- 函数关系的建立
- 数列极限与函数极限的定义及其性质
- 函数的左极限与右极限
- 无穷小量和无穷大量的概念及其关系
- 无穷小量的性质及无穷小量的比较
- 极限的四则运算
- 极限存在的两个准则:单调有界准则和夹逼准则
- 两个重要极限:\(\lim_{x \to 0} \frac{\sin x}{x} = 1\) 和 \(\lim_{x \to \infty} (1 + \frac{1}{x})^x = e\)
- 函数连续的概念
- 函数间断点的类型
- 初等函数的连续性
- 闭区间上连续函数的性质
2. 导数与微分
3. 积分
4. 常微分方程
5. 多元函数微分学
6. 多元函数积分学
7. 级数
8. 空间解析几何
9. 向量代数与解析几何
10. 多元函数的极值与最值
11. 重积分
12. 曲线积分与曲面积分
13. 场论初步
线性代数部分
1. 行列式
- 行列式的概念和基本性质
- 行列式按行(列)展开定理
2. 矩阵
- 矩阵的概念、线性运算、乘法、方阵的幂、方阵乘积的行列式、转置、逆矩阵的概念和性质、矩阵可逆的充分必要条件、伴随矩阵、初等变换、初等矩阵、矩阵的秩、矩阵的等价、分块矩阵及其运算
3. 向量空间
4. 线性变换
5. 特征值与特征向量
6. 二次型
7. 正定二次型
8. 线性方程组
9. 矩阵的对角化
10. 实对称矩阵的对角化
11. 二次型的标准形与规范形
12. 二次型的正定性判定
13. 线性空间的基本概念
14. 线性空间的同构与基变换
15. 线性空间的维数与基
16. 线性空间的子空间
17. 线性空间的直和与交和
18. 线性空间的同态与同构
19. 线性空间的泛性质
20. 线性空间的完备性与距离
21. 线性空间的内积空间
22. 内积空间的基与正交性
23. 内积空间的正交分解与标准正交基
24. 内积空间的谱定理
25. 内积空间的算子与本征值问题
26. 内积空间的特征值与特征向量问题
这些内容构成了2024年考研数学二的主要考试范围,考生应根据这些范围进行复习准备。
考研数学二真题
关于考研数学二的真题及答案解析,以下是一些可供下载的资源:
1. 真题合集(1980-2024年):提供了历年考研数学一、二、三的真题及解析,包含高清无水印的PDF版本。可以通过以下链接下载:https://zhentipdf.com/kaoyan/481.html 。
2. 历年真题及解析:该网站提供1980年至2024年的考研数学二真题及解析,适合考生复习使用。下载链接在文末:https://www.yanyoutong.com/thread-61-1-1.html 。
3. 2024年考研数学二真题:最新的2024年考研数学二真题及参考答案解析已发布,可以在中国教育在线获取:https://kaoyan.eol.cn/shiti/shuxue/202312/t20231226_2551145.shtml 。
4. 百度文库资源:提供2024年考研数学二真题的完整版,可以在百度文库查看和下载:https://wenku.baidu.com/view/be0b1e47baf3f90f76c66137ee06eff9aef849cc.html 。
这些资源将帮助你更好地备考考研数学二,祝你复习顺利!

 微信扫一扫打赏
微信扫一扫打赏
 支付宝扫一扫打赏
支付宝扫一扫打赏